 {width=50%}
{width=50%} Jamil Palacios Bhanji and Vanessa Lobue
Last edited Oct 19, 2022
make a folder for today's activity
make a "data" folder (inside the project folder)
For this activity, we will use the same Lumosity dataset from last week, but with one new (imaginary) variable: "eyesight". You can download the file lumos_subset1000pluseye.csv
make an "spss" folder (inside the project folder) for your SPSS files
If you have installed the PROCESS macro for SPSS, check that you see a menu item under Analyze->Regression called "Process v4.1 by Andrew Hayes" - if you installed it before and don't see it now, you may have to run SPSS as an administrator (right-click on SPSS icon and select "run as administrator") -- if you don't have admin access on your computer please join forces with a partner who has the process macro installed already. For instructions on installing PROCESS, see this video, first 4 minutes, and here is the link to download PROCESS https://www.processmacro.org/download.html
Data description: lumos_subset1000plusimaginary.csv is the same file we have been working with before. Today we will make use of a fabricated variable called imaginary_screensize which gives the size of the screen on which users complete the tests - this is a simulated variable that is not part of the real dataset.
This is subset of a public dataset of Lumosity (a cognitive training website) user performance data. You can find the publication associated with the full dataset here:
Guerra-Carrillo, B., Katovich, K., & Bunge, S. A. (2017). Does higher education hone cognitive functioning and learning efficacy? Findings from a large and diverse sample. PloS one, 12(8), e0182276. https://doi.org/10.1371/journal.pone.0182276
Import the data: Open SPSS and use File -> Import Data-> CSV or Text Data - now check the variable types and add labels if you wish. Careful! If you use "import text data" make sure you set the only delimiter as "comma" (SPSS may automatically also treat "space" as a delimiter, so uncheck that option)
What to do next:
ID, age, raw_score, imaginary_screensize, and eyesight_z, so you can ignore the other variables for this activity {width=50%}
{width=50%}
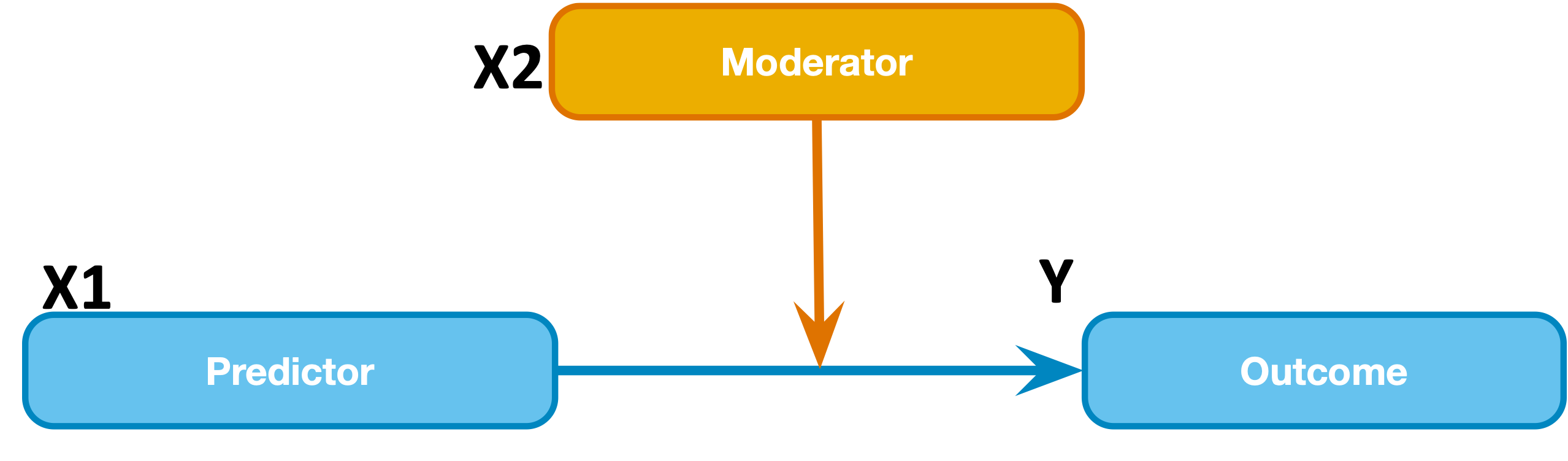
Above: the conceptual model of moderation
 {width=50%}
{width=50%}
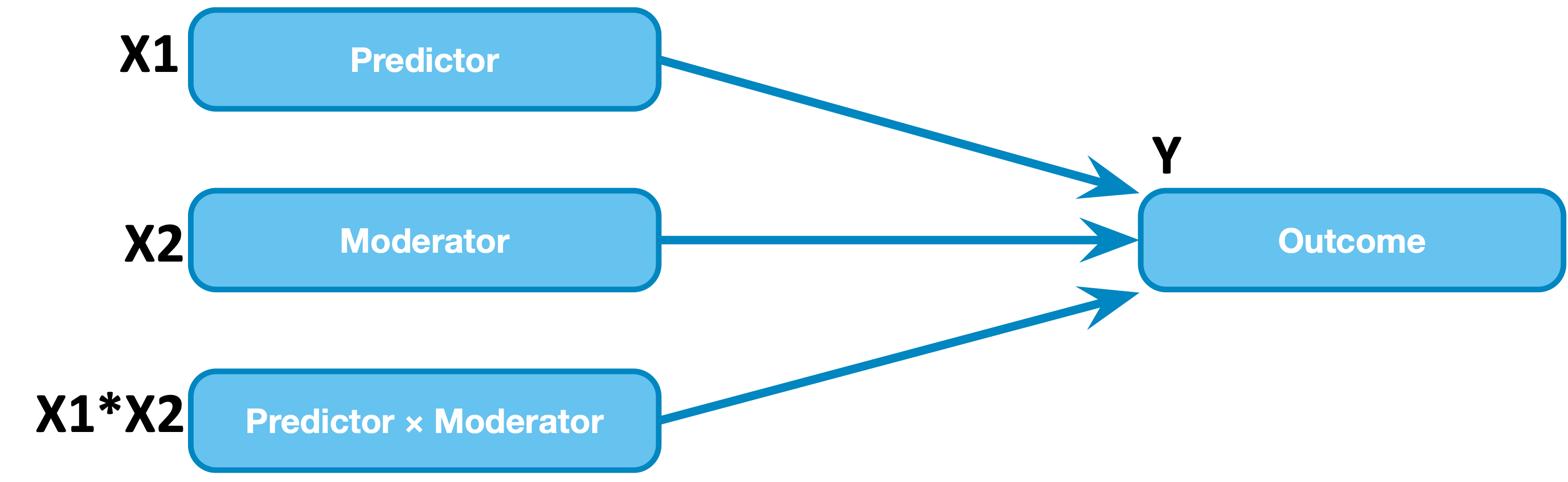
Above: the statistical model of moderation - notice that X1 and X2 are interchangeable in the statistical model (i.e., the statistical model does not distinguish between the predictor and the moderator)
Previously, when we looked just at age and raw_score, we saw a small association such that older participants scored lower. But what if that association depended on another variable, such as the size of their screen? That is, maybe older individuals do worse than younger individuals only if they are working on a small screen? Such a relationship would be an example of an interactive effect, or moderation (i.e., screen size moderates the effect of age on raw score, or it might equally be stated that age moderates the effect of screen size on raw score).
So far, the data we have worked with are real values from Lumosity, but for this step there is a simulated imaginary variable called imaginary_screensize - just for educational purposes. In the moderation model we will test, age is X1 (predictor), imaginary_screensize is X2 (moderator), and raw_score is Y (outcome).
As depicted in the statistical model of moderation graphic above, we test a moderation with a regression model where the outcome (Y) is explained by a predictor (X1), a moderator (X2), and their product (X1*X2, called the interaction of X1 and X2). To start out will use the same linear regression model that we were using last week.
Try it now:
1. First, create a new variable called ageXscreensize by using the Transform->Compute Variable menu (the Numeric Expression should be "age*imaginary_screensize")
2. Now go to Analyze->Regression->Linear and specify
raw_score as the Dependentage, imaginary_screensize, and your new variable ageXscreensize as Independents (all in Block 1)Scan through the Model Summary (we can reject the null hypothesis that all coefficients are zero) and then focus on the Coefficients Table. Notice that there are coefficient estimates for age, imaginary_screensize, and their interaction ageXscreensize.
The positive coefficient (with low p-value) for the interaction term suggests that at larger screensize values, the relation of age to performance is more positive (less negative to be precise) than at smaller screensize values. Equally, we could restate it: at older age values, the relation of screensize to performance is more positive/less negative. The coefficient for the interaction term has the same meaning as the other coefficients: that an increase in one unit of the predictor predicts an increase in .002 units of the outcome -- of course the predictor in this case is the product of two variables, so interpretation takes a little more work, which we will do in step 1.4.
But we now have issues with the interpretation of the coefficients for the main effects of age and imaginary_screensize. The coefficient for a single variable in a model represents the effect of that variable when other terms are zero. So the coefficient for imaginary_screensize (the main effect of screensize) now represents the effect of screensize at age=0. Likewise, the coefficient for age represents the effect of age when screensize=0. Neither effect is interpretable, because of the presence of the interaction.
If we subtract the mean age from each value of age and store it in a new variable called age_cent (and do the same for imaginary_screensize_cent), then we can enter these new variables into the regression instead. Then we will compute the interaction term as the product of these two centered variables. Then we will be able to better understand the resulting main effect coefficients (as, e.g., the effect of age at the mean value of screen size).
Create these new "centered" variables using SPSS Syntax (this is the easiest/quickest method given in SPSS documentation)
*Create new variables storing the means of original variables.
aggregate outfile * mode addvariables
/mean_age = mean(age)
/mean_screensize = mean(imaginary_screensize).
*Subtract mean from original values.
compute age_cent = age - mean_age.
compute screensize_cent = imaginary_screensize - mean_screensize.
compute age_centXscreensize_cent = age_cent * screensize_cent.
age_cent, screensize_cent, and age_centXscreensize_cent in your fileWe should have actually first selected only the cases that have valid values for all the columns we are using (age, imaginary_screensize, raw_score) - this is not really necessary because all cases have valid values in this data - but it is good practice to always be mindful of how many complete cases you have for a given set of variables, as it will affect calculations such as mean-centering (and you should always be watching out for and thinking about missing values).
Then run a new model that is the same as the last one except you use the centered variables (and interaction of the centered variables) as the predictors.
the model F-statistic didn't change, it is still significant (low p-value indicates the data and observed F-stat are unlikely under the null hypothesis [that the true value of all coefficients is zero] )
the coefficient (and statistics) for the interaction term didn't change (it is positive and the t-stat for the coefficient is the same), but the coefficients (and t-stats) for age_cent and screensize_cent differ from the uncentered version. When an interaction effect is included in a model, centering the variables allows us to interpret the main effects in these two ways (from Field textbook p.792): "(1) they are the effect of that predictor at the mean value of the sample; and (2) they are the average effect of the predictor across the range of scores for the other predictors" - Importantly, age is not a significant predictor in this model, meaning that if we hold screen size constant at its mean value then age is not significantly related to performance.
age) at different levels of another variable - (imaginary_screensize). We will calculate the effect of age at mean and +/- 1SD of imaginary_screensize - and this will give us an idea of how the effect of age varies at different levels of screensize. This is called a simple slopes analysis.raw_score as the Y variableage as the Ximaginary_screensize as the Moderator Wage predicts a decrease of .0422 units of raw_score.imaginary_screensize less than 4.81 units below the mean, the effect of age is significantly negative, and at values of imaginary_screensize more than 29.54 units above the mean, the effect of age is significantly positive.1) What is the relation between age and performance (raw_score) when screen size is held at a low value?
2) What is the relation between age and performance when screen size is held at its average (mean) value?
3) What is the relation between age and performance when screen size is held at a large value?
4) Can you translate those "significance regions" cutoffs into the original (not mean-centered) imaginary_screensize units?
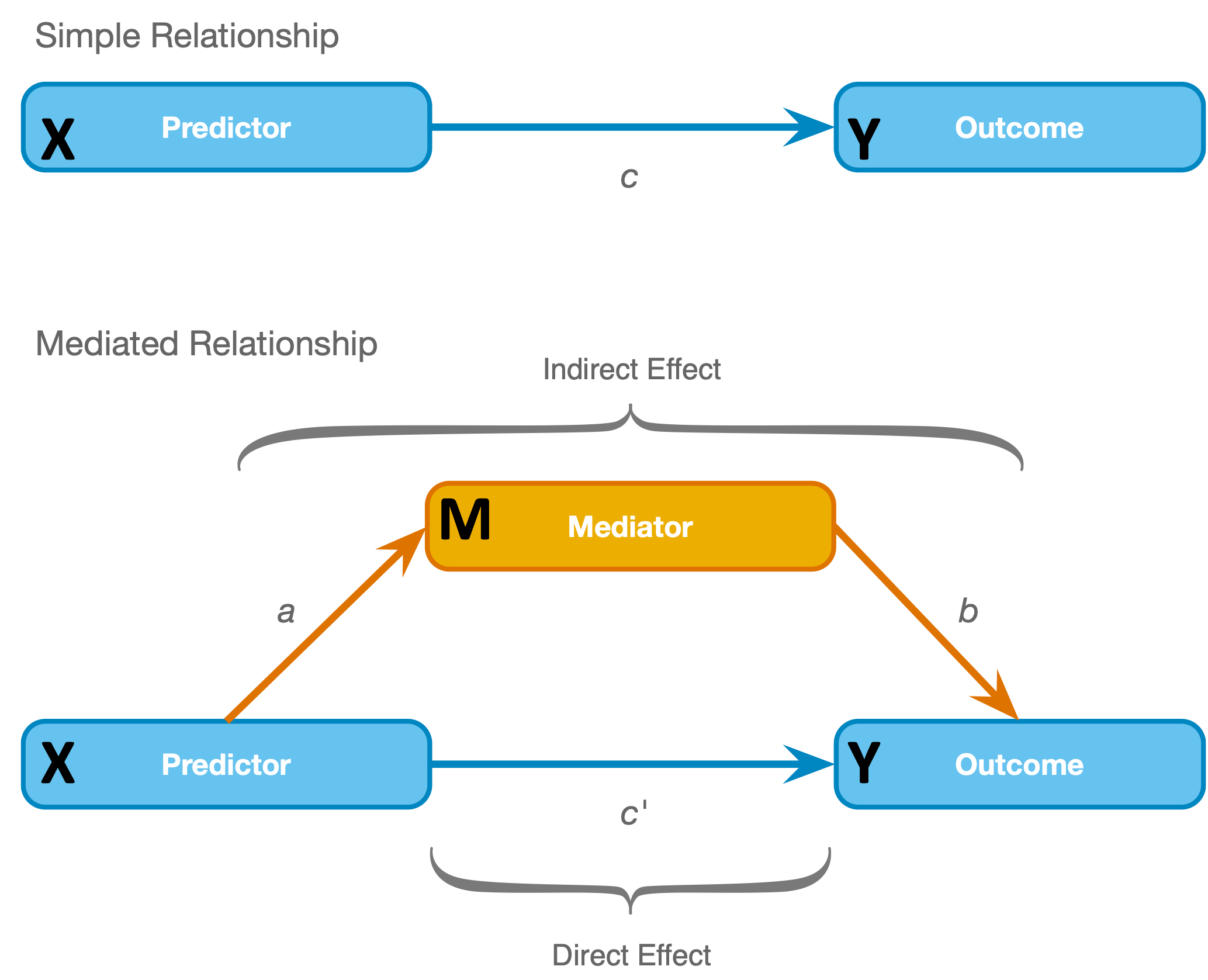
Above: the simple three variable model of mediation - notice that X and M are distinguished in the model (unlike X1 and X2 in the statistical moderation model)
Mediation refers to a situation when the relationship between a predictor variable (X in the chart above) and an outcome variable (Y in the chart above) can be explained by their relationship to a third variable (the mediator, M).
Forget about the screen size variable for a moment and consider possible explanations for the negative relation between age and performance that we saw when age was our only predictor for raw_score.
Maybe part of the relation could be explained by something like eyesight that deteriorates with age. The data file you imported for this activity has a new (simulated/imaginary) variable called eyesight_z which is an eyesight "score" where higher values indicate better eyesight (it has been scaled such that the sample mean is 0 and the s.d. is 1).
We will test a mediation model where eyesight_z explains the relation between age and raw_score.
A note about causality: In this model we have good reasons for thinking the direction of the relationships is as specified in the mediation model (i.e., it would not be possible for a change in eyesight to cause a change in age, or for a change in test performance to cause a change in eyesight) but there may be many unmeasured variables that could be involved. The test of our mediation model will tell us whether the eyesight_z measure accounts for a "significant" part of the relationship between age and raw_score.
There are the four conditions for our mediation model test, which are tested with three regression models. First we will list the regression models (coefficients of each model are different so we'll refer to them each with unique subscripts b1 through b4):
Y = intercept + b1XM = intercept + b2XY = intercept + b3X + b4MWe use these three models to check four conditions of mediation (section 11.4.2 of the Field textbook):
1. the predictor variable must significantly predict the outcome variable in model 1 (c is significantly different from 0)
2. the predictor variable must significantly predict the mediator in model 2 (a is significantly different from 0)
3. the mediator must significantly predict the outcome variable in model 3 (b is significantly different from 0)
4. the predictor variable must predict the outcome variable less strongly in model 3 than in model 1 (c' is closer to 0 than c, in other words, the direct effect is smaller than the total effect)
The PROCESS macro for SPSS gives us a bootstrapped 95% confidence interval around a*b, so if the interval does not contain zero, then we can say there is a significant mediation (or, more precisely, we reject the null hypothesis that the indirect effect is zero). Bootstrapping involves taking thousands of repeated random samples of cases from our data (with replacement, so the same case can be included more than once in one repetition) and building a sampling distribution of our parameter of interest from those random samples (they are samples of a sample, hence the term "bootstrapping"). From that sampling distribution we can estimate our parameter of interest (a*b) and a confidence interval around it.
Now let's assess our mediation model (that eyesight_z explains the relation between age and raw_score)
Note that we are using a series of linear regression models to test the mediation model, so the assumptions that we need to check are the same ones we discussed in the multiple regression lab activity, and the same as the ones we should have checked in the moderation examlpe above (but also notice that we will be using bootstrapping to estimate the mediated effect, which eases concern over significance tests on the parameter estimate when assumptions are violated). We won't check assumptions here (to save a little time) but it is a good exercise check the plots of residuals from each model if you have extra time.
X corresponds to age, Y to raw_score, and M to eyesight_z, so the three models we use to test the conditions are:
1. raw_score = intercept + b1age [b1 = path c]
2. eyesight_z = intercept + b2age [b2 = path a]
3. raw_score = intercept + b3age + b4eyesight_z [b3 = path c' and b4 = path b]
Go to Analyse->Regression-> "Process v4.0 by Andrew Hayes":
- specify raw_score as the Y variable
- specify age as the X
- specify eyesight_z as the M
- make sure to remove imaginary_screensize as the Moderator W if it is still in their from before
- select Model number 4 (this refers to Hayes' label for a mediation model, unrelated to our description of the 3 regression models that are used to test a mediation)
- Under Options, select "Show total effect model ..."
- Under Options, select "Standardized effects ..."
- Under Long variable names, select "accept the risk", but be warned that the first 8 characters of any variable names in the dataset must be unique
- Click OK to estimate the models (this will run the three regression models that we discussed above as required for evidence of mediation)
Let's look closely at the output from top to bottom:
OUTCOME VARIABLE: eyesight corresponds to model #2 of the three models we use to test the mediation.coeff value for the age row gives us b2 (path a)LLCI and ULCI columns give us the lower (LLCI) and upper (ULCI) limits of the 95% confidence interval around each parameterOUTCOME VARIABLE: raw_scor corresponds to model #3 of the three models we use to test the mediation.
coeff for age gives us b3 a.k.a path c' a.k.a. the direct effectcoeff for eyesight gives us b4 a.k.a. path bTOTAL EFFECT MODEL corresponds to model #1 of the three models we use to test the mediationcoeff for age gives us b1 a.k.a path c a.k.a. the total effect (it's the same as the coefficient we got last week when we entered age as the only predictor for raw_score)at this point, take a moment to recognize that the first three of our four conditions are satisfied (a, b, and c are significantly different from 0)
now look at the section starting "TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y"
age predicts a -.0276 change in raw_score, considering the indirect path onlyage predicts that much decrease in raw_score through the indirect path onlyWhat is the indirect effect of age on performance, through eyesight (path a*b)? (coefficient, standard error of the coefficient, confidence interval around the coefficient)
imaginary_screensize in a mediation model?The "Completely standardized indirect effect(s) of X on Y" section produced by PROCESS is essentially a standardized regression coefficient, and as such it can be compared across studies (and is useful for meta-analyses). We could try to also compute something similar to R2, but approaches to do so cause difficulties with how we interpret them, so we recommend the standardized indirect effect measure (see the Field textbook section 11.4.3 for full discussion).