Data day 1 - notes on the analyses in SPSS

2024-03-21

Atiyah's data

Research question:

• How does self-esteem alter the use of affect as information?
  

Description of the data/study

Human participants listened to 12 audio recordings of baby cries that varied in intensity. Participants heard each cry and rated how distressed the infant was in each cry. After hearing all cries, participants reported how much the cries upset them. Additionally, participants completed a self-esteem measure (10-item Rosenberg).

Variables

outcome:
- crytotl (how distressed were the infants)

IV/explanatory variables:
- esteem (self esteem)
- upset (how much did the cries upset you?)

Hypothesis

Affect is more positively related to judgments of the babies' distress in high, compared to low, self-esteem individuals. (esteem moderates the relation of upset to crytotl)

What statistical test to use?

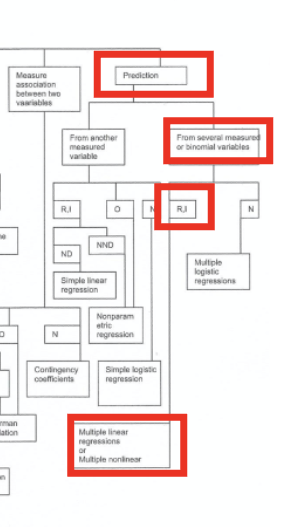
Multiple linear regression.

Inclusion/exclusion

• Female - exclude non-Female participants
• check complete cases (how many?) - 47 complete (5 missing from 52 total Female)
  

Examine variable distributions

• crytotal - pretty much normal, one low value
  
• upset - pretty much normal
  
• esteem - left skew (ceiling, restricted range?)
  

Specify the model and estimate parameters

• crytotl ~ upset_cent + esteem_cent + upsXest
  
• center variables? Yes
  

NHST

null hypotheses (full model test) - the specified model describes the data no better than the null model (mean only) R-squared tells us the full model explains .388 of the variance in distress ratings
F-stat tells us that the model fit to the data is unlikely (p<.001 if there is model is not better than the null)
coefficient for the interaction is .223, p = .01, telling us it is unlikely we would observe a coefficient at least as large if there is no true interaction effect.

Visualization

One approach to visualize an interaction between two continuous variables is to choose low, medium, and high values of the moderator, and plot the predicted association between predictor and outcome at each of those levels (see the "moderation and mediation" activity in R):

1. Go to the PROCESS menu (under Regression) and specify your model (model number 1 for this interaction effect)
   
2. Don't use the paste option through the GUI! (otherwise the syntax will get filled with internal PROCESS code and freeze up your SPSS)
   
3. Estimate the model.
   
4. For plotting code, you must now respecify the model in SPSS syntax, like this:
   process y=crytotl /x=upset /w=esteem /plot=1 /model=1.
   

Reporting

• full model F, p, R²
• interaction term coefficient, std err of coefficient (or CI), t-stat (df is N - #parameters estimated, don't forget to count the intercept), p
• if meaningful, you could also report primary effect at meaningful levels of the moderator

The full regression model included distress judgment of baby cries (mean across all cries) as the outcome, with explanatory variables of negative affect, self-esteem and the interaction of both. The full model fit the data better than the null model (F(3,43) = 9.092, p < .0001, R² = .388). The interaction term was significant (beta = 0.223 std. error = 0.083, t(43) = 2.693, p = .01).